Basel Problem in Python

Introduction to Basel Problem in Python

Welcome to the fascinating world of the Basel problem in Python! If you’ve ever been intrigued by the convergence of infinite series, you’re in for a treat. In this comprehensive guide, we’ll embark on a journey to understand the Basel problem, its historical significance, and how Python can be leveraged to explore and solve this mathematical puzzle.

Understanding the Basel Problem

Unraveling the Mystery

The Basel problem, first posed by Pietro Mengoli in 1650 and later solved by Leonhard Euler in 1734, is a classic mathematical question that revolves around the convergence of an infinite series. The problem is as follows:

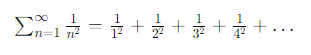
The challenge lies in determining the exact value to which this infinite series converges. Euler’s groundbreaking solution revealed that the Basel problem converges to π^2/6

Python and the Basel Problem

Cracking the Code

Now, let’s dive into the exciting part – implementing the Basel problem in Python. We’ll use Python’s simplicity and power to explore the convergence of the series.

def basel_problem(limit):
    result = 0
    for n in range(1, limit + 1):
        result += 1 / (n ** 2)
    return result

# Example: Calculate the Basel problem value for the first 100 terms
result_100 = basel_problem(100)
print(f"The Basel problem value for the first 100 terms is approximately {result_100}")

In this code snippet, the basel_problem function calculates the sum of the series up to a given limit. You can easily adjust the limit parameter to explore the convergence for different numbers of terms.

The Significance of Euler’s Solution

Euler’s Brilliance Unveiled

Leonhard Euler’s solution to the Basel problem not only provided a numerical answer but also introduced the concept of convergent infinite series. Euler’s brilliance laid the foundation for further developments in the field of mathematical analysis.

Exploring Convergence Rate

Python for Numerical Exploration

One of the exciting aspects of using Python for the Basel problem is the ability to visualize the convergence rate. Let’s create a Python script to generate a plot showcasing how quickly the series converges.

import matplotlib.pyplot as plt

def visualize_convergence(limit):
    results = []
    for n in range(1, limit + 1):
        results.append(basel_problem(n))
    
    plt.plot(range(1, limit + 1), results, marker='o')
    plt.axhline(y=(3.141592653589793238**2)/6, color='r', linestyle='--', label=r'$\frac{\pi^2}{6}$')
    plt.title('Convergence of Basel Problem Series')
    plt.xlabel('Number of Terms')
    plt.ylabel('Sum of Series')
    plt.legend()
    plt.show()

# Example: Visualize convergence for the first 100 terms
visualize_convergence(100)

This script uses the matplotlib library to create a plot illustrating how the sum of the series approaches Euler’s solution as we include more terms.

Python Libraries for Advanced Analysis

Taking it to the Next Level

For advanced mathematical analysis and symbolic computation, Python offers libraries like SymPy. Let’s extend our exploration using SymPy to symbolically represent the sum of the Basel problem series.

import sympy as sp

def symbolic_basel_problem(limit):
    n = sp.symbols('n')
    series = sp.summation(1/n**2, (n, 1, limit))
    return series

# Example: Symbolic representation for the sum of the first 10 terms
symbolic_result = symbolic_basel_problem(10)
print(f"The symbolic representation of the sum of the first 10 terms is: {symbolic_result}")

By leveraging SymPy, we can obtain symbolic expressions, enabling a deeper understanding of the mathematical properties involved.

Conclusion to Basel problem in Python

In conclusion, the Basel problem in Python offers a captivating exploration of mathematical concepts, historical significance, and programming implementation. From Euler’s ingenious solution to leveraging Python for numerical analysis, this guide has provided a comprehensive understanding of the Basel problem.

As you continue your journey into the world of mathematical exploration with Python, remember that the Basel problem is just one of many fascinating challenges waiting to be unraveled through the lens of code. Happy coding!

If you face any issue regarding this article i.e in reading or understanding it so please contact me as soon as possible or ask me a question in comment section.

Website Link: https://Codelikechamp.com

Medium Link: Follow me on Medium

Linkedin Link: Follow me on Linkedin

Facebook Group: Join our Facebook Group

4. Image Alt Text:

Include descriptive alt text for images, especially in the visualizations section.

Basel Problem in Python